La fórmula divina
La sorprendente belleza de un número irracional
El número áureo pertenece al conjunto de los número irracionales, esto es, aquellos que no pueden expresarse como cociente de dos número enteros. Por ejemplo, la raíz cuadrada de dos es irracional -un descubrimiento que incomodó de tal modo a los pitagóricos que lo ocultaron al mundo-. En nuestro caso, el número áureo lo podemos computar con una calculadora si seguimos estas sencillas instrucciones: primero, calculamos la raíz cuadrada de 5; luego sumamos 1 al resultado y el total lo dividimos por 2. Si sabemos programar un ordenador, podemos intentar batir el récord del mayor número de decimales calculados: en el año 2000 y con menos de 3 horas de computación, se encontraron los primeros 1.500 millones de cifras decimales.
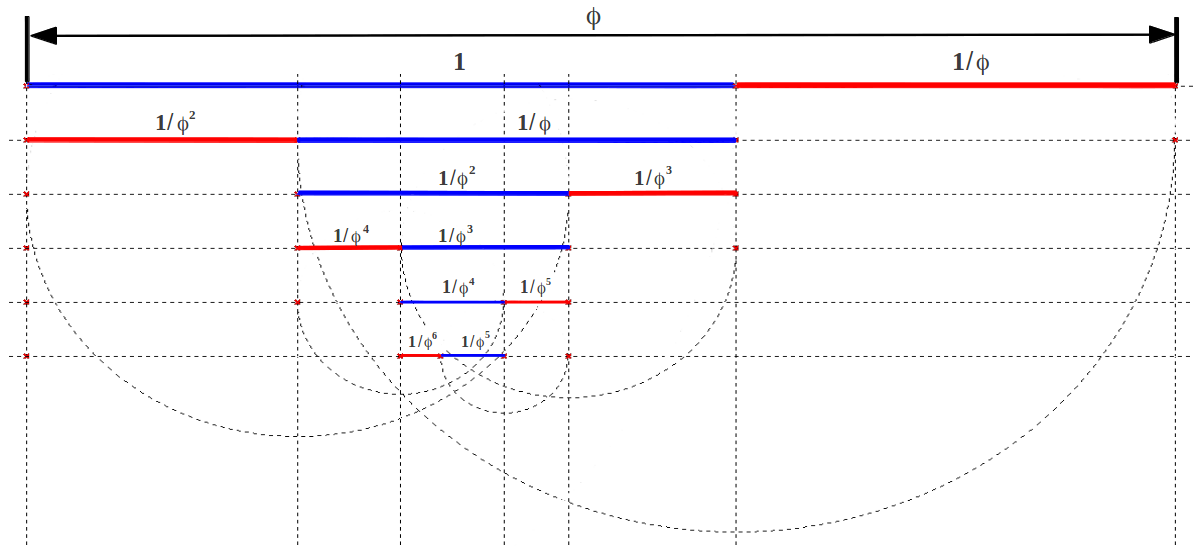
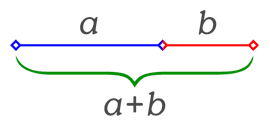
Matemáticamente hablando, podemos definir el número áureo como aquél que si le sumamos uno sale el mismo resultado que si lo elevamos al cuadrado. Así, si el 4 fuera el número áureo, para calcular su cuadrado no haría falta hacer la operación de 4 por 4, que sale 16, sino que simplemente bastaría con sumarle 1. Y es que en realidad existen dos números aúreos, uno positivo (1,618033...) y otro negativo (-1,618033...), pero es el primero el que se ha llevado toda la gloria.
El humanista que puso nombre al 1,618033...
Hasta aquí todo esto puede parecernos pura numerología. Es como si alguien, con muy poco trabajo y mucho tiempo libre, se hubiera tomado la molestia de empezar a buscar relaciones curiosas con los números. Sin embargo, lo verdaderamente misterioso es que ese número tan extraño lo encontramos en el crecimiento de las plantas, en las piñas, en la distribución de las hojas en un tallo o en la formación de las caracolas. También en el carné de identidad, las tarjetas de crédito, gran parte de las tarjetas de presentación y en casi todas las cajetillas de tabaco. O en el Partenón. O en el ejemplo clásico de lo que es un cuerpo armonioso: el Hombre de Vitrubio de Leonardo da Vinci.
Siguiendo los pasos de quienes más le influyeron, el humanista Leon Battista Alberti y el escultor Antonio Filarete, Leonardo creía que la anatomía y la arquitectura estaban relacionadas. Fue en la década de 1480, mientras trataba de ganarse al duque de Milán y a los arquitectos de la corte, cuando profundizó en esta relación que expresó en su famoso dibujo de 1487, basado claramente en la descripción del arquitecto Marcus Vitruvius Pollio.
La perfección anatómica es la perfección áurea
En ella, Pollio afirma: "En el cuerpo humano, la parte central es el ombligo. Pues si un hombre se tumba boca arriba, con los brazos y las piernas extendidas, y se centran un par de compases en el ombligo, los dedos de las manos y los pies tocarán la circunferencia descrita a partir de ese centro. Y también puede inscribirse en una figura cuadrada". Si dividimos el lado del cuadrado (la altura del ser humano) por el radio de la circunferencia (la distancia del ombligo a la punta de los dedos) tendremos el número áureo. Así, si el lector quiere saber si es bellamente perfecto, sólo tiene que coger una regla.
Poco a poco Leonardo se fue obsesionando con la búsqueda de pautas que relacionaran no sólo la anatomía con la arquitectura, sino con la estructura armónica de la música y con la propia naturaleza. Su búsqueda de proporciones en el mundo que le rodeaba, al igual que su intento de relacionar la circunferencia de las copas de los árboles con la longitud de sus ramas, fue intensa pero vana. No obstante, no era una idea errónea, porque mirando la naturaleza podemos encontrar el número áureo en diferentes contextos. Pero antes debemos echar la vista atrás y prestar atención a un matemático italiano del siglo XIII que tenía una pasión un tanto oscura por los conejos y su tasa reproductiva.
El número más bello en una madriguera de conejos
En 1202, Leonardo Fibonacci se preguntaba acerca de cuán rápido se expandirían los conejos por la Tierra en condiciones ideales. Supongamos, se dijo, que tenemos una única pareja, que ambos miembros están preparados para procrear al mes de existencia y que dan a luz a una nueva pareja tras un mes de gestación. ¿Cuántas parejas habrá al cabo de un año? Al final del primer mes la pareja original está dispuesta a procrear, pero sigue habiendo una única pareja. Al final del segundo mes tendremos la original y su primera pareja-hija. Al finalizar el tercero habrá en el campo la original, la primera pareja, que ya está a punto para procrear, y una segunda pareja-hija. Al terminar el cuarto mes tendremos la original y su tercera pareja-hija, la primera pareja y su primera pareja-hija, y la segunda pareja-hija, que ya está dispuesta para procrear. En definitiva, la sucesión de parejas de conejos es: 1, 1, 2, 3, 5. ¿Es capaz de adivinar el lector el patrón que se esconde tras esa sucesión? Si la alargamos un poco resulta más fácil: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233... En efecto, la llamada sucesión de Fibonacci, también denominada números de Fibonacci, se obtiene sumando los dos previos para obtener el siguiente. Ahora bien, ¿qué tiene que ver esta sucesión de números con el número áureo? Haga el siguiente experimento: coja una calculadora y divida uno cualquiera por su inmediato anterior. A medida que progrese en la sucesión, el cociente se irá acercando más y más al número áureo.
En términos matemáticos, esto quiere decir que la sucesión de números creada dividiendo un número de Fibonacci por su inmediato anterior tiende, o tiene como límite, el número áureo. Esto es, esta sucesión infinita de números termina, en el infinito, en el número áureo.
El pedigrí del zángano sigue un modelo matemático
El problema con los conejos de Fibonacci es que son ideales. ¿Existe algún ejemplo más realista de que esta sucesión áurea se encuentre en la naturaleza? Sí, por ejemplo en el árbol familiar de cualquier zángano de un panal. Éste nace del huevo no fertilizado de la reina, luego tiene una madre, pero no tiene padre. Por el contrario, tanto la reina (la única que puede poner huevos) como las obreras nacen del huevo fertilizado por un macho. Tienen, por tanto, padre y madre. Teniendo esto en mente, el árbol familiar de un zángano queda como sigue: tiene 1 madre, 2 abuelos (macho y hembra), 3 bisabuelos (dos de la familia de la abuela y uno de la del abuelo), 5 tatarabuelos, 8 tataratatarabuelos... ¡El árbol genealógico del zángano es una sucesión de Fibonacci! Y no sólo eso. En 1966, Doug Yanega, del Museo de Investigación Entomológica de la Universidad de California, descubrió que la relación que existe entre abejas hembras y machos en una comunidad es cercana al número áureo.
La espiral logarítmica de la concha del nautilo
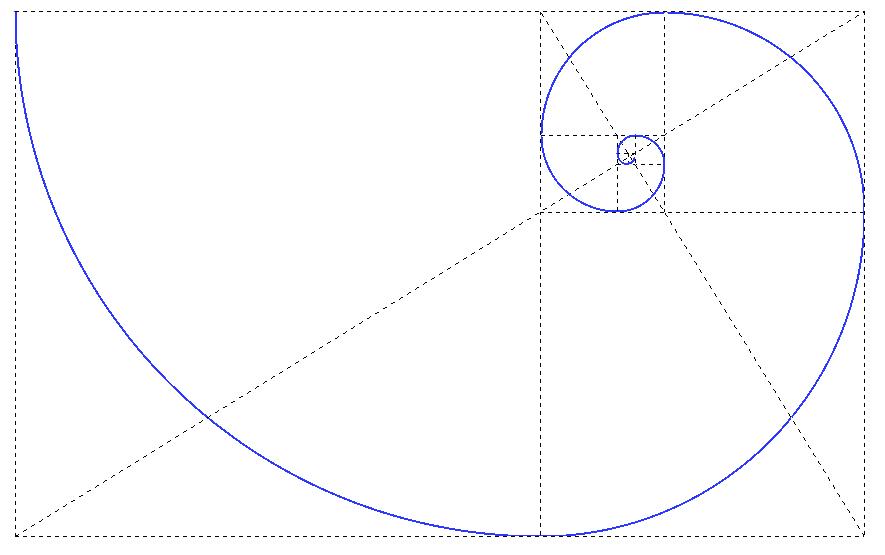
Convirtamos ahora los números en cuadrados. Pongamos dos iguales, uno junto a otro, de cualquier tamaño, cuyos lados tomaremos como unidad. Encima de ellos, dibujemos otro cuyo lado sea el doble de los anteriores. A la derecha, añadamos otro más, con el triple de lado. Debajo, el correspondiente a 5, y así sucesivamente, de modo que cada nuevo cuadrado tenga de lado la suma de los dos cuadrados anteriores. Si ahora dibujamos un cuarto de circunferencia dentro de cada cuadrado (empezando por el primero), como en la fotografía de la caracola del comienzo del reportaje, tendremos una espiral logarítmica que es, justamente, la que presenta la concha del nautilo.
Ahora coja un lápiz y trace una línea que vaya desde el centro al exterior. Fíjese en dos puntos en los que esta línea corte a la concha, con la única condición de que la espiral haya dado una vuelta completa entre ambos. Comprobará que el más exterior está 1,618 veces más lejos del centro que el del interior. Esto quiere decir que el factor de crecimiento de la concha es el número áureo.
Los números de Fibonacci también los encontramos en el número de espirales a la izquierda y a la derecha que podemos contar en las semillas de los girasoles y en las piñas de los pinos; en el número de pétalos de las flores (3 el iris; 5 o bien 8 en algunos ranúnculos; las margaritas y girasoles suelen contar con 13, 21, 34, 55 ó 85...) y en el número de flores en las espirales de la coliflor y del brécol. De hecho, cada uno de ellos es una diminuta coliflor en sí misma. Si cuenta las espirales en ambas direcciones que salen de esas miniflores, ¿qué número le sale? Puede buscar así mismo números de Fibonacci en el plátano y en la manzana. Incluso las hojas alrededor del tallo siguen este orden.
El mejor sistema de ordenación posible
¿Por qué este gusto de la naturaleza por la sucesión de Fibonacci? Hojas, pétalos y semillas se ordenan en las plantas siguiendo un ángulo fijo porque éste es el mejor sistema de empaquetamiento aunque la planta crezca. Si colocamos el número áureo de hojas por vuelta en el tallo obtenemos el mejor empaquetamiento para que reciban todas ellas el máximo de luz sin que unas se oculten a otras y, en el caso de las flores, la mejor exposición paras atraer a los insectos polinizadores. Los números de Fibonacci son la mejor aproximación que existe al número áureo. Visto todo esto, no resulta sorprendente que el Partenón pueda enmarcarse en un rectángulo áureo -aquél en el que el cociente de su longitud por su altura sale el número áureo-. Igual sucede con las tarjetas de crédito. ¿Acaso hay algo más bello que una Visa sin límite de gasto?La arquitectura de la Divina Proporción
El Partenón de Atenas -bajo estas líneas- es un buen ejemplo de belleza arquitectónica griega y, como tal, se puede enmarcar dentro de un rectángulo áureo. Algunos matemáticos han pretendido ver el número áureo en la Gran Pirámide de Keops -a la derecha-. Así, si se divide la distancia que hay desde la base de una de las caras de la pirámide hasta el vértice superior por la altura de la pirámide se obtiene 1,6. ¿Se trata quizá de algo intencionado? Algunos piensan que sí, pero lo cierto es que no hay base alguna para pensar en ello. El papiro Rhind (1650 a. de C.), uno de los trabajos matemáticos más antiguos que se conservan, no menciona el número áureo, a pesar de que resuelve algunos problemas relacionados con la construcción de pirámides.Fibonacci, el hombre de los conejos
Leonardo de Pisa es mejor conocido por su apodo, Fibonacci (de filius Bonacci, hijo de Bonacci). Nacido en el norte de Italia, pero educado en el norte de África, pasó toda su juventud viajando por el Mediterráneo, pues su padre era el representante de los comerciantes de la República de Pisa.Fue uno de los primeros en introducir el sistema de numeración decimal en Europa. En 1202 publicó su Liber abacci (Libro de Calcular), donde explicaba cómo sumar, restar, dividir y multiplicar con este nuevo sistema. Fue aquí donde aparece la que hoy es su famosa sucesión. Lo curioso es que fue presentado como un problema planteado para que los lectores aprendieran a usar el sistema decimal, y no como consecuencia de sus reflexiones sobre aritmética.Miguel Ángel Sabadell