Métodos de construcción geométrica

Hay muchas formas de dividir un segmento geométricamente siguiendo la Proporción Áurea.  En el primero (Método A, Figura 4) tan solo necesitas calcular el punto medio de un segmento dos veces: empezando por el segmento AA', se calcula su punto medio M. Entonces se marca el punto B de forma que el segmento MB tenga la misma longitud que AA', y se calcula su punto medio M'. Por último, se marca el punto C tal que M'C=MB y esto es todo. Uno acaba con un segmento AC que está dividio según los Segmentos Aureos AB y BC. Es decir,

$$\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AC}}{\mathrm{AB}}=\phi$$

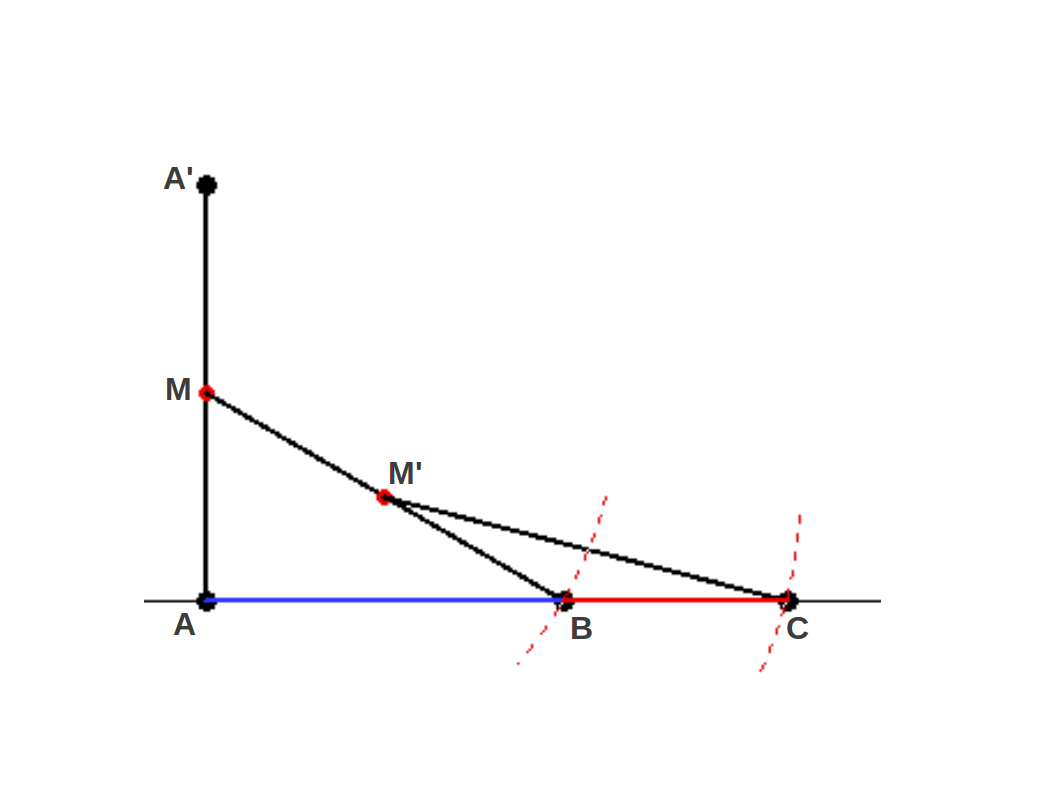Figura 4: METODO A: Construcción geométrica de la Proporción Aurea usando dos puntos medios. Con este método, no se sabe a priori la longitud del segmento AC.

Los otros dos métodos tienen en común el uso de un triángulo 1-1/2 (es decir, un triángulo rectángulo con un cateto de longitud doble del otro). En el método B se empieza por el segmento AC y se calcula su punto medio M (Figura 5). Entonces se levanta la mitad de ese segmento perpendicularmente a MC para obtener el punto C' y el triángulo 1-1/2 ACC' (cuya diagonal es $\sqrt{5}\mathrm{/2}$). Entonces se lleva la altura del triángulo sobre la hipotenusa AC' para obtener el punto B', y por último se lleva la longitud AB' hacia abajo para obtener el punto B, que divide el segmento original AC según la Proporción Aurea, con lo cual tenemos de nuevo:

$$\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AC}}{\mathrm{AB}}=\phi$$

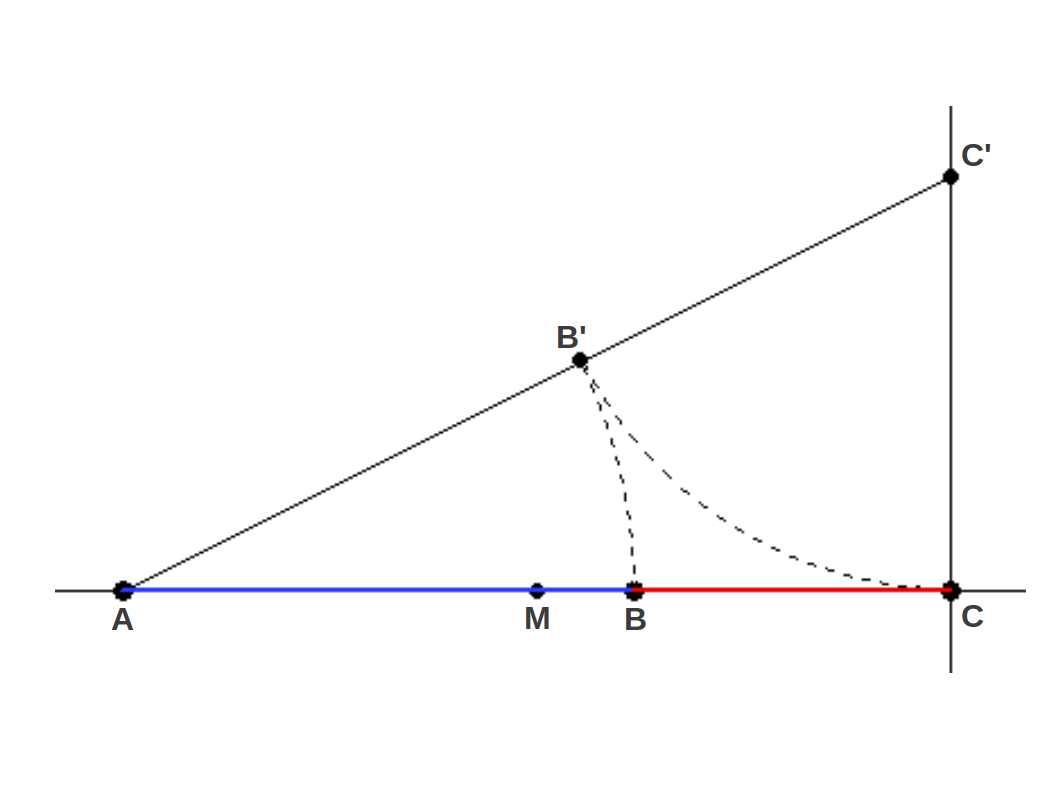Figura 5: METODO B: División geométrica de un segmento según la Proporción Aurea usando dos arcos. El segmento original acaba dividido en dos partes Aureas.

El tercer método (método C) empieza por un cuadrado de lado AB (Figura 6). Se calcula el punto medio de este lado y se dibuja un círculo con centro en este punto pasando por D hasta encontrar el punto C. Y ya lo tenemos: el segmento AC está dividido según la Proporción Aurea en el punto B, así que tenemos de nuevo

$$\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AC}}{\mathrm{AB}}=\phi$$

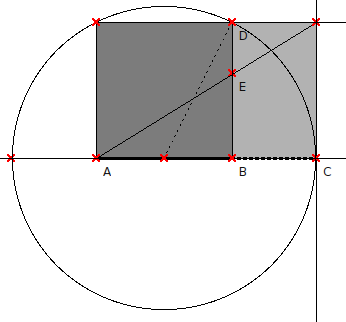Figure 6: METODO C: Determinación geométrica de un segmento AC tal que AB y BC están en Proporción Aurea. El proceso produce un Rectángulo Aureo, que contiene un cuadrado y un Rectángulo Aureo más pequeño dentro.

El tercer método tiene la ventaja de que se acaba con un Rectángulo Aureo, eso es, un rectángulo cuyos lados están relacionados por la Proporción Aurea. Y este proceso se puede iterar indefinidamente sin necesidad de ningún nuevo círculo, simplemente dibujando las diagonales de cada rectángulo. Por ejemplo el rectángulo Aureo pequeño de la Fig.6 (gris claro) contiene un rectángulo Aureo aún menor determinado por el punto E, que divide el lado BD en dos partes Aureas BE y ED (el lector debe notar que en un rectángulo general las longitudes BE y BC no son necesariamente iguales, mientras que en un rectángulo Aureo sí lo son). Así pues, cada nuevo rectángulo Aureo en este proceso iterativo se compone de un cuadrado y un nuevo rectángulo Aureo menor. Este proceso constructivo permite construir la Espiral Aurea:

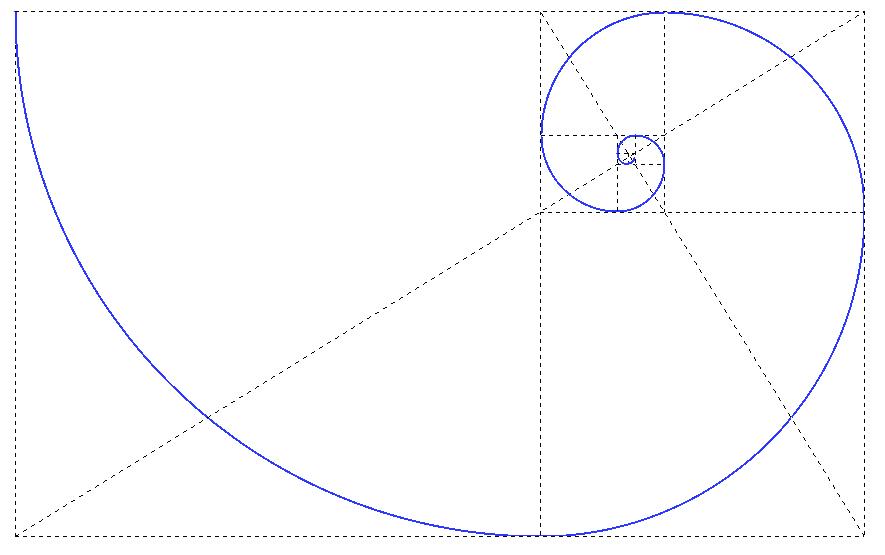Figura 7: La Espiral Aurea

Información recuperada de: http://www.sacred-geometry.es/?q=es/content/la-proporci%C3%B3n-aurea