La Proporción Áurea en el pentágono

El pentágono es el polígono regular que contiene de forma natural la Proporción Aurea. Parafraseando a Lawlor [1] "el pentágono [es] el símbolo de la vida, con su simetría quíntuple que sólo aparece en los organismos vivos". En realidad el pentágono podría definirse como el polígono regular de cinco lados cuyas diagonales están en Proporción Aurea con sus lados. Esta propiedad proporciona un método directo de construir un pentágono como se muestra en la figura siguiente: 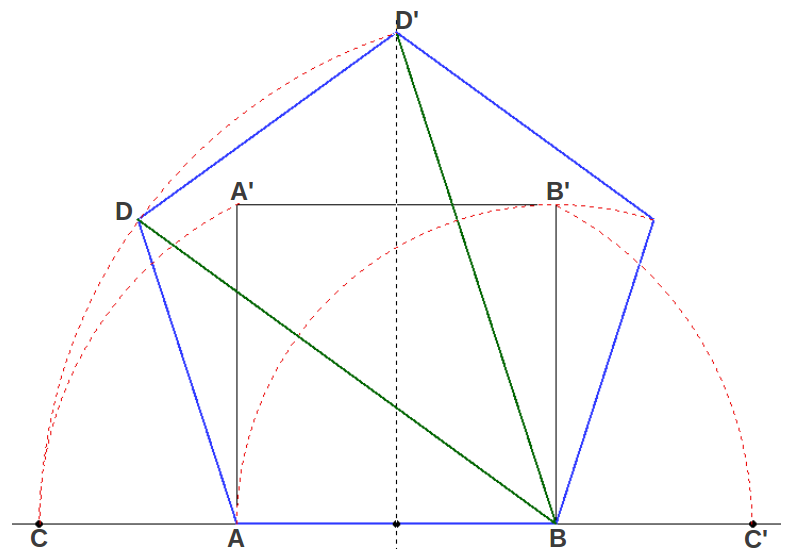Figura 11: La construcción del pentágono a partir de la Proporción Aurea. Empezando por el lado AB, se calculan los puntos C y C' que extienden este segmento en Proporción Aurea (CB/AB = AC'/AB = φ). Entonces la longitud BC se convierte en la diagonal del pentágono (por ejemplo BD y BD' en la figura) y permite localizar sus vértices (Figura 11). El Triángulo Aureo y el Gnomon Aureo están contenidos de forma natural dentro del pentágono (Figura 12). Esto demuestra de una forma diferente que en el pentágono la razón entre la diagonal y el lado es φ. 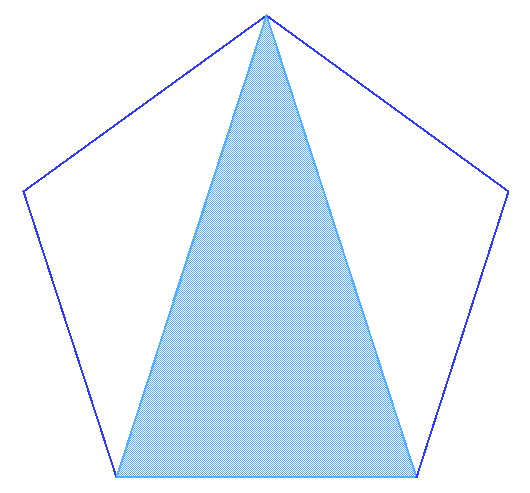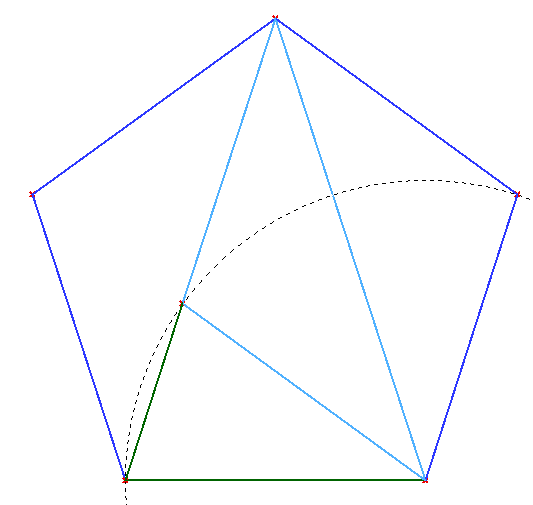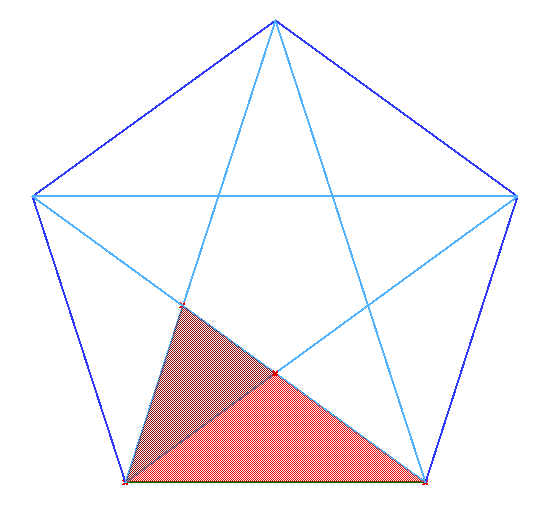(a) Triángulo Aureo en el pentágono (b) Gnomon Aureo en el pentágono Figura 12 Cuando se dibujan todas la diagonales del pentágono se consigue un pentagrama. El pentagrama muestra que el Gnomon Aureo, y por lo tanto la Proporción Aurea, están contenidos iterativamente dentro del pentágono (Figura 13). 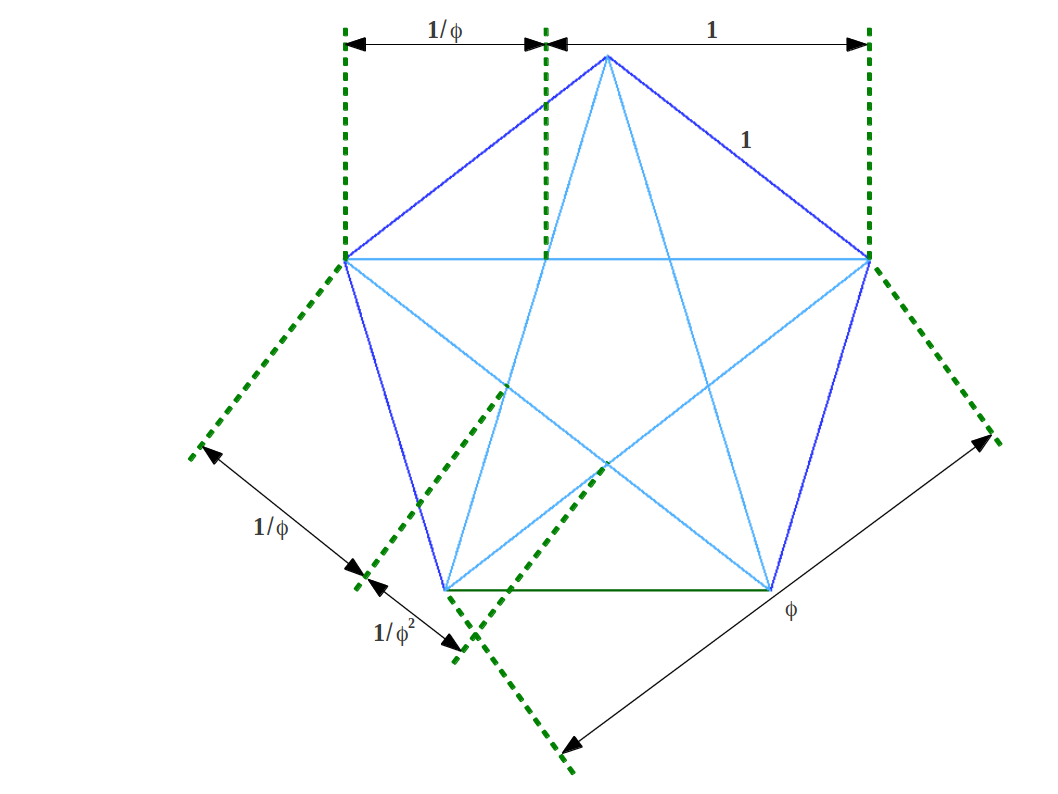(a) Gnomons Aureos iterados en el pentágono. (b) Proporciones sucesivas en Proporción Aurea en el pentagrama. Figure 13
Información tomada de: http://www.sacred-geometry.es/?q=es/content/la-proporci%C3%B3n-aurea